Questão 136 - Matemática

Uma indústria faz uma parceria com uma distribuidora de sucos para lançar no mercado dois tipos de embalagens. Para a fabricação dessas embalagens, a indústria dispõe de folhas de alumínio retangulares, de dimensões 10 cm por 20 cm. Cada uma dessas folhas é utilizada para formar a superfície lateral da embalagem, em formato de cilindro circular reto, que posteriormente recebe fundo e tampa circulares. A figura ilustra, dependendo de qual das duas extensões será utilizada como altura, as duas opções para formar a possível embalagem.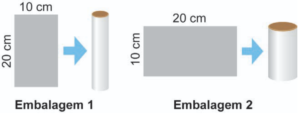" alt="enem 2024 cinza regular q136 img01" width="300" height="114" srcset=" 300w, 768w, 791w" sizes="(max-width: 300px) 100vw, 300px" />

Dentre essas duas embalagens, a de maior capacidade apresentará volume, em centímetro cúbico, igual a